Formelhefte S2

Følger, rekker og lån

Følger og rekker

En tallfølge er en ordnet liste med tall: $a_{1}, a_{2}, a_{3}, a_{4}, \dots, a_{n}$

En rekke er summen av tallene i en tallfølge. Delsummen $s_{n}$ av de $n$ første leddene i en følge er gitt ved

s_{n} = \sum_{i = 1}^{n} a_{i} = a_{1} + a_{2} + a_{3} + a_{4} + \dots + a_{n}

Table: Formler til følger og rekker

Forklaring	Formel
Ledd i aritmetisk følge (rekursiv)	$a_{n + 1} = a_{n} + d$
Ledd i aritmetisk følge (eksplisitt)	$a_{n} = a_{1} + (n - 1) \cdot d$
Ledd i geometrisk følge (rekursiv)	$a_{n + 1} = a_{n} \cdot k$
Ledd i geometrisk følge (eksplisitt)	$a_{n} = a_{1} \cdot k^{n - 1}$
Aritmetisk rekke (sum av følge)	$s_{n} = \frac{a_{1} + a_{n}}{2} \cdot n$
Geometrisk rekke (sum av følge)	$s_{n} = a_{1} \cdot \frac{k^{n} - 1}{k - 1}$
Uendelig geometrisk rekke	$- 1 < k < 1 ⟹ s = \frac{a_{1}}{1 - k}$

Rekker og konvergens

En rekke konvergerer og har summen $s$ dersom summen $s_{n}$ av $n$ første leddene nærmer seg tallet $s$ når $n \to \infty$ . Altså

lim_{n \to \infty} s_{n} = s

En enkel tommelfingerregel for å sjekke om en rekke konvergerer er å sjekke om leddene går mot 0 når $n \to \infty$ . Dersom rekka ikke konvergerer, så divergerer den. Det er umulig å finne summen til en divergerende rekke fordi summen ikke eksisterer.

Uendelige geometriske rekker

Geometriske rekker er alltid konvergente når kvotiententen $k \in ⟨ - 1, 1 ⟩ ⟺ - 1 < k < 1$ . Summen av denne typen rekker er gitt ved formelen

s = \frac{a_{1}}{1 - k}

En uendelig geometrisk rekke kan ha en kvotient $k (x)$ som er en funksjon av $x$ istedenfor å ha et fast tall $k$ som kvotient. Slike rekker har et konvergensområde i de intervallene av $x$ hvor $- 1 < k (x) < 1$ .

Summen av slike rekker er gitt ved en funksjon $s (x)$ som har samme definisjonsmengde som konvergensområdet.

s (x) = \frac{a_{1}}{1 - k (x)}, x \in konvergensområdet

Programmering av følger og rekker

Ifølge læreplanen skal dere utforske rekursive sammenhenger med programmering. En rekursiv sammenheng vil si at vi bruker ett ledd til å regne ut det neste leddet – for å regne ut $a_{n + 1}$ så trenger vi først å ha regnet ut $a_{n}$ .

Ledd i aritmetisk tallfølge

# Regner ut de første leddene i en aritmetisk tallfølge
# med a_0 = 0 og d = 2.
a = 0 
d = 2
n = 10
for i in range(1, n + 1):
	print(f"a_{i} = {a}")
	a = a + d

Ved bruk av print(f"") så kan vi blande tekst og variabler. Variablene skriver vi med krøllparenteser slik: {variabelnavn}.

Delsum av geometrisk rekke

# Regner ut de første leddene og delsummene i geometrisk rekke med a_0 = 1 og k = 1.5
a = 1 
k = 1.5
delsum = a
n = 10
for i in range(1, n + 1):
	print(f"a_{i} = {a:.2f}. s_{i} = {delsum:.2f}")
	a = a * k
	delsum = delsum + a

Her bruker vi en teller, delsum, som i hver omgang av for-løkka blir oppdatert med den nye summen.

Vi kan avrunde desimaltall med {variabelnavn:.2f} der 2-tallet er antallet desimaler vi ønsker.

Eksempel med følge som ikke er geometrisk eller aritmetisk

Oppgavetekst: Gitt følgende tallfølge: $1, 3, 4, 8, 15, 27, 50, \dots$

De 3 første leddene i denne følgen er spesielle. Deretter følger tallene et fast mønster.

Lag et program som skriver ut de første n leddene i denne følgen. Hvis programmet ditt fungerer riktig vil du få $a_{50} = 11986911799691$ .

Etter å ha funnet ut at $a_{4} = a_{1} + a_{2} + a_{3}$ og $a_{5} = a_{4} + a_{3} + a_{2}$ så kan vi tenke oss fram til at mønsteret i følgen er

a_{n} = a_{n - 1} + a_{n - 2} + a_{n - 3}, n \geq 4

Vi kan programmere dette på følgende måte

a_minus3 = 1
a_minus2 = 3
a_minus1 = 4
n = 50

for i in range(4, n + 1):
  a = a_minus3 + a_minus2 + a_minus1
  print(f"a_{i} = {a}")
  a_minus3 = a_minus2
  a_minus2 = a_minus1
  a_minus1 = a_i

Her oppdaterer vi hele tiden verdiene av de tre foregående leddene.

Vi kan også løse den samme oppgaven ved bruk av lister. Her bruker vi metoden append på lista a. Dette legger til et nytt element i slutten av lista. Dette nye elementet skal være lik summen av de tre foregående leddene.^[1]

a = [1, 3, 4]
antall_ledd = 50
for i in range(4, antall_ledd+1):
  a.append(a[i-2] + a[i-3] + a[i-4])
print(a)

Nåverdi og lån

Table: Ordliste med begreper knyttet til lån og nåverdi

Begrep	Forklaring
Rentefot/-sats	Hvor mange prosent rente vi må betale per år
Terminer	Antall innbetalinger
Lånebeløp	Størrelsen på lånet da du tok det opp
Restlån	Størrelsen på lånet i dag
Terminbeløp	Hvor mye penger du betaler i hver termin
Renter	Den delen av terminbeløpet som dekker rentene
Avdrag	Den delen av terminbeløpet som betaler ned på lånet
Termingebyr	Bankens gebyr for å sende ut faktura

Nåverdi

Nåverdi forteller oss hvor mye et fremtidig (eller fortidig) beløp er verdt i nåtidens penger. Det er vanlig at penger blir mindre og mindre verdt for hvert år siden vi forventer avkastning på investeringene våre.

Nåverdien $N$ til et fremtidig beløp $B$ er gitt ved

N = \frac{B}{v^{n}}

Der $v$ er vekstfaktoren til kalkulasjonsrenta og $n$ er antall perioder. Hvis du vil finne nåverdien til et beløp bakover i tid så velger du en negativ verdi for $n$ .

Serielån

I et serielån er alle avdragene like store, men rentene minker og derfor minker også terminbeløpene.

Vi finner avdragene med

avdrag = \frac{lånebeløp}{antall terminer}

Vi finner terminbeløpene med

terminbeløp = avdrag + rente av restlånet

Terminbeløpene danner en aritmetisk rekke hvor terminbeløp nummer $n$ er gitt ved

T_{n} = T_{1} + (n - 1) \cdot (avdrag \cdot \frac{rentefot}{100})

Annuitetslån

I et annuitetslån er alle terminbeløpene like store. Rentene synker i løpet av nedbetalingsperioden og avdragene øker. Lånebeløpet $L$ skal være lik summen av nåverdiene av terminbeløpene:

L = \sum_{i = 1}^{n} \frac{T}{v^{i}}

Der $T$ er terminbeløpet og $v$ er vekstfaktoren til kalkulasjonsrenta.

Legg merke til at dette er en geometrisk rekke med $k = \frac{1}{v}$ . Mange oppgaver med annuitetslån på del 2 kan løses ved å sette opp likningen over i CAS.

Vi kan også bruke formler til å regne ut terminbeløpene eller lånebeløpet til et annuitetslån. Lånebeløpet $L$ er terminfaktoren $F$ multiplisert med terminbeløpet $T$ .

L = F \cdot T

Vi finner terminfaktoren ved hjelp av følgende formel hvor $v$ er vekstfaktoren til renta per termin og $n$ er antall terminer

F = \frac{1 - \frac{1}{v^{n}}}{v - 1}

Funksjonsdrøfting

Funksjonsdrøfting handler om å finne ut hvordan funksjoner ser ut når du tegner dem.

Nullpunkter finner du ved å sette $f (x) = 0$
Topp-, bunn- og terrassepunkter finner du ved å sette $f^{'} (x) = 0$
Vendepunkter finner du ved å sette $f^{″} (x) = 0$
Monotoniegenskaper (når funksjonen vokser og synker) finner du ved å sjekke når $f^{'} (x) > 0$ og $f^{'} (x) < 0$ . Du trenger å faktorisere og tegne fortegnslinje for å finne ut av dette.
Krumning finner du ved å sjekke når $f^{″} (x) > 0$ og $f^{″} (x) < 0$ . Du trenger å faktorisere og tegne fortegnslinje for å finne ut av dette.

Husk også disse viktige sammenhengene

Stigningstallet til tangenten i punktet $(a, f (a))$ er lik den deriverte i punktet $f^{'} (a)$ .
En funksjon har sin maksimalverdi i toppunktene eller randpunktene
En funksjon har størst vekstfart i vendepunktene.

Logaritmer

Egenskaper ved logaritmefunksjoner

En logaritmefunksjon er den inverse funksjonen til en eksponentialfunksjon.

Eksponentialfunksjonen $f (x) = 10^{x}$ har tilhørende logaritmefunksjon $\log_{10} x$ eller ofte bare kalt $\log x = \lg x$ .
Eksponentialfunksjonen $f (x) = e^{x}$ har tilhørende logaritmefunksjon $\ln x$
Eksponentialfunksjonen $f (x) = a^{x}$ har tilhørende logaritmefunksjon $\log_{a} x$ for $a > 0$ . Du kan altså velge hvilket som helst positivt tall $a$ som base i logaritmefunksjonen.

Siden logaritmefunksjonen og eksponentialfunksjonene er inverse så vil disse nulle hverandre ut:

\begin{aligned} \ln e^{x} = x & ⟺ e^{\ln x} = x \\ \log 10^{x} = x & ⟺ 10^{\log x} = x \\ \log_{a} a^{x} = x & ⟺ a^{\log_{a} x} = x \end{aligned}

Logaritmefunksjonene er definert for alle positive tall slik at definisjonsmengden blir $D_{f} = ⟨ 0, \infty ⟩$ .

Vi velger som oftest den naturlige logaritmen, $\ln x$ , i S2 siden denne er enklere å derivere og integrere enn de andre logaritmene.

Regneregler for logaritmer

Her bruker jeg den naturlige logaritmen som eksempel, men disse reglene gjelder for alle typer logaritmer.

Table: Regneregler for logaritmer

Forklaring	Formel
Bruke logaritme på likning	$a = b ⟺ \ln a = \ln b$
Hente ned eksponent	$\ln a^{x} = x \ln a$
Logaritme til produkt	$\ln (a \cdot b) = \ln a + \ln b$
Logaritme til kvotient	$\ln \frac{a}{b} = \ln a - \ln b$
Nullpunkt til logaritmer	$\ln 1 = 0$

Merk at den siste regelen forteller oss at alle typer logaritmefunksjonene har sitt eneste nullpunkt i $x = 1$ . For $f (x) = \ln x$ vil funksjonen være negativ for $0 < x < 1$ og positiv for alle $x > 1$ .

Rasjonale funksjoner

En rasjonal funksjon består av en brøk med polynomfunksjoner i teller og nevner:

f (x) = \frac{P (x)}{Q (x)}

Rasjonale funksjoner har følgende egenskaper:

Nullpunkt når telleren $P (x) = 0$
Bruddpunkt når nevneren $Q (x) = 0$
Definisjonsmengden er alle $x$ bortsett fra bruddpunktet: $D_{f} = R ∖ {x_{bruddpunkt}}$

Asymptoter

Asymptoter er tenkte linjer som en funksjon nærmer seg. Asymptoter kan være horisontale, vertikale eller skrå.

Vi får vertikale asymptoter i bruddpunktene. Vi finner disse ved å løse $Q (x) = 0$ .
Vi får en horisontal asymptote dersom $P$ og $Q$ har samme grad. Vi finner den horisontale asymptoten ved å sammenligne leddene i $P$ og $Q$ med høyest grad, og dividere koeffisientene foran disse leddene på hverandre. For eksempel gir funksjonen $\frac{2 x^{2}}{4 x^{2}}$ asymptoten $y = \frac{2}{4} = \frac{1}{2}$ .
Vi får skrå asymptoter når graden av $P$ er én større enn graden av $Q$ . Vi finner denne ved å beregne $P (x) : Q (x)$ med polynomdivisjon. Den skrå asymptoten er svaret på divisjonen når du ser bort fra resten.

Derivasjon

Definisjon: Hvis $f (x)$ er kontinuerlig i et punkt $x$ så er den deriverte i punktet:

f^{'} (x) = lim_{Δ x \to 0} \frac{f (x + Δ x) - f (x)}{Δ x}

Den deriverte i et punkt er lik den momentane vekstfarten i punktet og dermed også lik stigningstallet til tangenten til $f$ i punktet.

Derivasjonsregler

Table: Formler for derivasjon

Forklaring	Funksjon	Derivert
Konstant	$k$	$0$
Potensfunksjon	$x^{r}$	$r \cdot x^{r - 1}$
Konstante koeff.	$k \cdot g (x)$	$k \cdot g^{'} (x)$
Summer	$g (x) \pm h (x)$	$g^{'} (x) \pm h^{'} (x)$
Produkt	$u (x) \cdot v (x)$	$u^{'} (x) \cdot v (x) + u (x) \cdot v^{'} (x)$
Kvotienter	$\frac{u (x)}{v (x)}$	$\frac{u^{'} v - u v^{'}}{v^{2}}$
Eksponentialfunk	$e^{x}$	$e^{x}$
Eksponentialfunk	$a^{x}$	$a^{x} \ln a$
Logaritme	$\ln x$	$\frac{1}{x}$
Kjerneregelen	$g (u (x))$	$g^{'} (u) \cdot u^{'} (x)$

Huskeregel kjerneregelen: Multipliser den deriverte av den ytre funksjonen med den deriverte av kjernen.

Den deriverte av ln x

(\ln (x))^{'} = \frac{1}{x}

Merk at selv om $g (x) = \frac{1}{x}$ er definert for $x \in R ∖ {0}$ så er den deriverte av logaritmefunksjonen kun definert for $x > 0$ .

Funksjonen $f (x) = \ln x$ har definisjonsmengde $D_{f} = ⟨ 0, \to ⟩$ . Derfor kan ikke den deriverte ha noe større definisjonsmengde enn dette. For å kunne derivere en funksjon så må den være kontinuerlig i punktet. For $\ln x$ sin del gir det ikke mening å snakke om vekstfarten i $x = - 2$ siden $f (- 2)$ ikke eksisterer.

Stigningstall og tangenter

Stigningstallet, $a$ , til tangenten til $f (x)$ i punktet ved $x = x_{1}$ er lik den deriverte i punktet, $f^{'} (x_{1})$ . For å finne likningen til tangenten kan vi sette inn kjente tall i likningen for rett linje

y = a x + b

Vi kan også bruke ettpunktsformelen hvor $y_{1} = f (x_{1})$

y - y_{1} = a (x - x_{1})

Integrasjon

Ubestemte integraler

Et ubestemt integral er å finne alle antideriverte $F (x)$ til en funksjon $f (x)$ slik at $F^{'} (x) = f (x)$ .

Table: Formler for integrasjon

Forklaring	Funksjon	Integrert
Konstant	$k$	$k x + C$
Koeffisient	$k \cdot f (x)$	$k \cdot \int f (x) d x$
Flere ledd	$f (x) \pm g (x)$	$\int f (x) d x \pm \int g (x) d x$
Potensfunksjon	$x^{r}$	$\frac{1}{r + 1} x^{r + 1} + C, r \neq - 1$
Spesialtilfelle	$\frac{1}{x} = x^{- 1}$	$\ln \| x \| + C, x \neq 0$
Eksponentialfunksjon	$e^{k x}$	$\frac{1}{k} e^{k x} + C$
Naturlig logaritme	$\ln x$	$x \cdot \ln x - x + C$
Eksponentialfunksjon^[2]	$a^{x}$	$\frac{1}{\ln a} a^{x} + C, a > 0 \land a \neq 1$

Bestemt integral som grense av sum

Vi har en funksjon $f (x)$ og vi ønsker å finne arealet under grafen fra $x = a$ til $x = b$ .

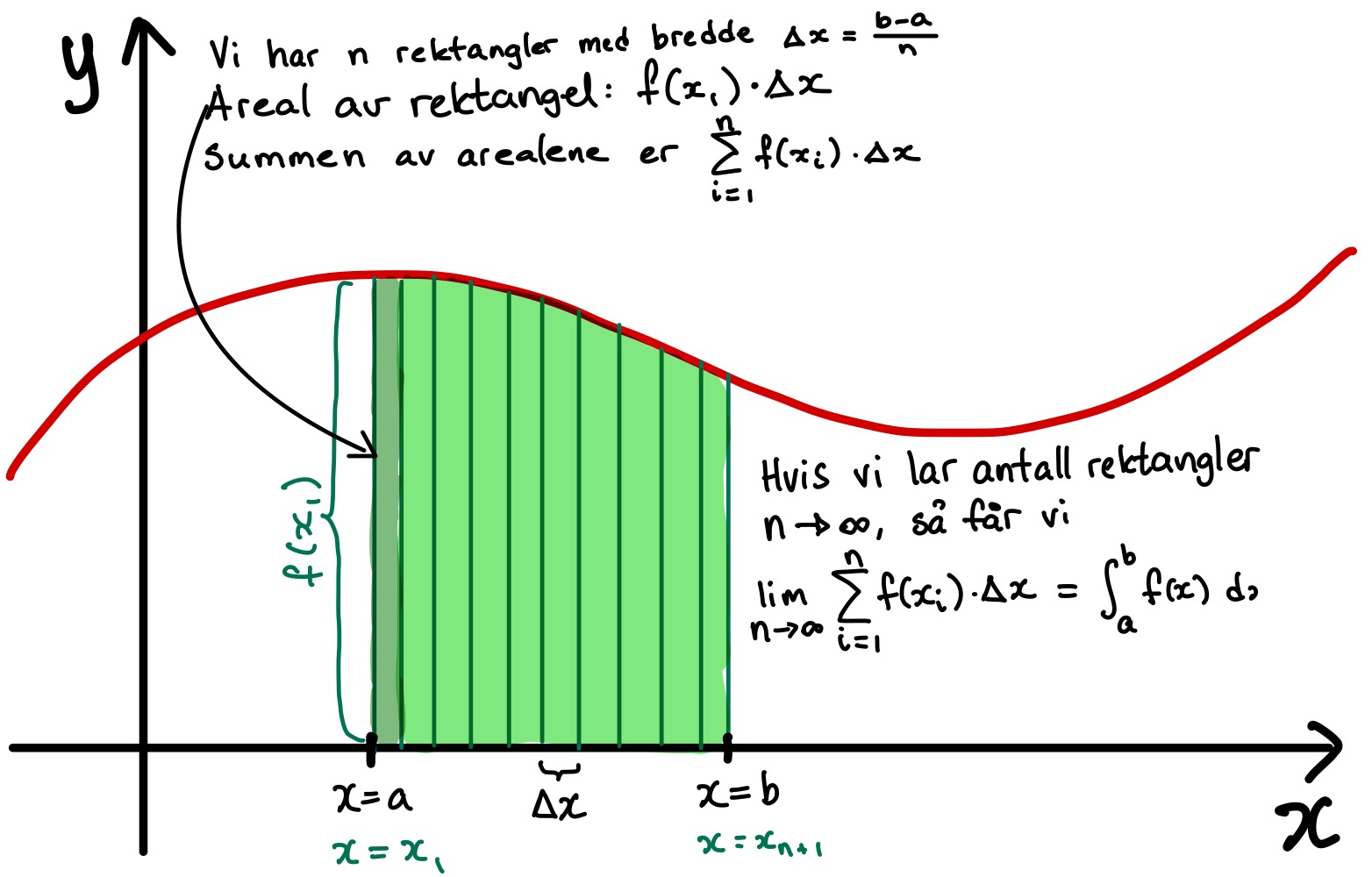
Det bestemte integralet er summen av uendelig mange rektangler under grafen

Vi forsøker å dele opp området under grafen i $n$ rektangler. Bredden på hvert rektangel må da være $Δ x = \frac{b - a}{n}$ .

Hvis vi kaller $x$ -verdien i starten av rektangelet for $x_{i}$ der $i \in {1, 2, 3, \dots, n}$ så vil høyden av hvert rektangel være $f (x_{i})$ .

Siden arealet til et rektangel er høyde multiplisert med bredde vil summen av arealene til rektanglene altså være

S_{n} = f (x_{1}) \cdot Δ x + f (x_{2}) \cdot Δ x + f (x_{3}) \cdot Δ x + \dots = \sum_{i = 1}^{n} f (x_{i}) \cdot Δ x

Hvis vi lar bredden av rektanglene bli veldig små slik at rektanglene egentlig bare blir infitesimalt smale striper får vi

lim_{Δ x \to 0} S_{n} = lim_{n \to \infty} \sum_{i = 1}^{n} f (x_{i}) \cdot Δ x = \int_{a}^{b} f (x) d x

Fundamentalsetningen

Fundamentalsetningen eller analysens fundamentalteorem forteller oss at integrasjon og derivasjon er motsatte operasjoner.

Fundamentalsetningen del 1

La $f$ være en kontinuerlig funksjon på $[a, b]$ . La

F^{'} (x) = f (x) for alle x \in [a, b]

Denne førsten delen av fundamentalsetningen forteller oss at alle kontinuerlige funksjoner $f$ har antideriverte funksjoner $F$ .

Fundamentalsetningen del 2

Gitt $f$ fra del 1 så er

\int_{a}^{b} f (x) d x = {[F (x)]}_{a}^{b} = F (b) - F (a)

Denne andre delen av fundamentalsetningen forteller oss at vi kan beregne et bestemt integral ved hjelp av det ubestemte integralet

Areal under grafer

La $f (x)$ være en funksjon som er positiv for alle $x \in [a, b]$ . Da er arealet, $A$ , av flatestykket som er avgrenset av grafen til en funksjon $f (x)$ , $x$ -aksen og linjene $x = a$ og $x = b$ lik integralet av

A = \int_{a}^{b} f (x) d x

Dersom grafen ligger under $x$ -aksen så er arealet gitt ved

A = - \int_{a}^{b} f (x) d x

Dersom funksjonen krysser $x$ -aksen i intervallet $[a, b]$ , så er du nødt til å dele opp integralet ved nullpunktene og legge sammen summene av arealene.

Areal mellom grafer

Hovedprinsippet for å finne arealet mellom grafer er å ta integralet av den øverste grafen og trekke fra integralet fra den nederste grafen.

La $f$ og $g$ være to funksjoner. For å finne arealet, $A$ , av flatestykket mellom grafene er du først nødt til å finne skjæringspunktene mellom grafene ved å løse likningen $f = g$ .

Areal mellom grafer med to skjæringspunkter

Dersom du får to løsninger $x_{1}$ og $x_{2}$ fra likningen $f = g$ så er arealet

A = \int_{x_{1}}^{x_{2}} (f (x) - g (x)) d x der f \geq g for alle x \in [x_{1}, x_{2}]

Dersom $g \geq f$ på intervallet $[x_{1}, x_{2}]$ så må du bytte om på rekkefølgen av leddene i integranden til $(g (x) - f (x))$ .

Areal mellom grafer med tre eller flere skjæringspunkter

Hvis du har tre eller flere skjæringspunkter mellom $f$ og $g$ så er du nødt til å dele opp integralet i flere deler. La oss si at du får de tre løsningene $x_{1}$ , $x_{2}$ og $x_{3}$ fra likningen $f = g$ . Hvis $f \geq g$ for $x \in [x_{1}, x_{2}]$ og $g \geq f$ for $x \in [x_{2}, x_{3}]$ så kan du finne det samlede arealet med følgende formel

A = \int_{x_{1}}^{x_{2}} (f (x) - g (x)) d x + \int_{x_{2}}^{x_{3}} (g (x) - f (x)) d x

Integrasjonsteknikker

Delvis integrasjon

Delvis integrasjon brukes ofte dersom du skal integrere et produkt av ulike to ulike funksjoner. Du kan gjerne tenke på delvis integrasjon som en omvendt produktregel for derivasjon.

Delvis integrasjon er spesielt nyttig dersom den ene faktoren er enkel å integrere og den andre faktoren er enkel å derivere.

Sett den ene faktoren til å være $u$ , dette er den faktoren som blir derivert. Den andre faktoren setter setter du lik $v^{'}$ . Deretter bruker du formelen nedenfor.

\int u \cdot v^{'} d x = u \cdot v - \int u^{'} \cdot v d x

DI-metoden for delvis integrasjon

Det er også mulig å bruke oppsettet kalt DI-metoden. Eksempelet under viser DI-metoden for $\int x^{2} e^{2 x} d x$ . Du lager en tabell med tre kolonner.

Den første kolonnen viser fortegnet. Dette veksler mellom $+$ og $-$ .
Den andre kolonnen inneholder faktoren som skal deriveres (D). For hver rad så deriverer du faktoren.
Den tredje kolonnen inneholder faktoren som skal integreres (I). For hver rad så integrerer du faktoren.

	D	I
$+$	$x^{2}$	$e^{2 x}$
$-$	$2 x$	$\frac{1}{2} e^{2 x}$
$+$	$2$	$\frac{1}{4} e^{2 x}$
$-$	$0$	$\frac{1}{8} e^{2 x}$

Svaret med DI-metoden finner du ved å starte på fortegnet oppe til venstre ( $+$ ), gå en til høyre ( $x^{2}$ ) og deretter på skrå ned til høyre ( $\frac{1}{2} e^{2 x}$ i raden under). Bruk $+$ som fortegnet og multipliser de to faktorene slik at du får $+ x^{2} \cdot \frac{1}{2} e^{2 x}$ . Du fortsetter på samme måte nedover. Svaret på oppgaven vår blir

+ x^{2} \frac{1}{2} e^{2 x} - 2 x \frac{1}{4} e^{2 x} + 2 \frac{1}{8} e^{2 x} + C = \frac{1}{2} e^{2 x} x^{2} - \frac{1}{2} e^{2 x} x + \frac{1}{4} e^{2 x} + C

Du lager rader i tabellen fram til du får en null, eller helt til du ser at du kan integrere produktet av faktorene i en rad. Hvis du ser at du kan integrere produktet av faktorene i en rad (for eksempel kan vi integrere produktet av 2 og $\frac{1}{4} e^{x}$ i rad 3), så kan du sette opp følgende

+ x^{2} \frac{1}{2} e^{2 x} - 2 x \frac{1}{4} e^{2 x} + \int 2 \frac{1}{4} e^{2 x} d x = \frac{1}{2} e^{2 x} x^{2} - \frac{1}{2} e^{2 x} x + \int \frac{1}{2} e^{2 x} d x

Når du løser dette vil du få samme svar som tidligere.

Variabelskifte

Variabelskifte brukes hvis du skal integrere en sammensatt funksjon. Variabelskifte kalles ofte for den omvendte kjerneregelen.

Velg en del av integranden som $u$ , dette er variabelskiftet ditt.
Deriver $u$ slik at du finner $u^{'} = \frac{d u}{d x}$ .
Løs likningen med hensyn på $d x$ slik at du får $d x = \frac{d u}{u^{'}}$
Substituer $d x$ med $\frac{d u}{u^{'}}$ i det opprinnelige uttrykket ditt.
Substituer inn $u$ i integranden.
Integrer uttrykket som nå har formen $\int g (u) d u$
Substituer ut alle $u$ i svaret med det opprinnelige uttrykket for $u$

Variabelskifte – se etter en faktor du kan derivere

Dersom du kan derivere en av faktorene i integranden, og den deriverte blir lik en annen faktor i integranden så bør du bruke variabelskifte. Ta for deg følgende regnestykke

\int \frac{\ln x}{x} d x

Vi vet at ${(\ln x)}^{'} = \frac{1}{x}$ , dermed er $\ln x$ et svært godt valg for variabelskifte.

Vi setter $u = \ln x$ og skriver den deriverte av $u$ som $\frac{d u}{d x}$

\begin{aligned} u & = \ln x \\ u^{'} = \frac{d u}{d x} & = \frac{1}{x} \\ d u & = \frac{1}{x} d x \\ d x & = x \cdot d u \end{aligned}

Vi kan nå bytte ut $d x$ i integranden med $x \cdot d u$ og vi får

\int \frac{u}{x} x d u = \int u d u = \frac{1}{2} u^{2} + C

Vi bytter tilbake $\ln x$ for $u$ og får svaret

\frac{1}{2} (\ln x)^{2}

Delbrøkoppspalting

Kommer dette på eksamen?

Jeg vet ikke om det er nødvendig å kunne delbrøkoppspalting til del 1 av eksamen. Hvis du sikter mot karakteren 6 så ville jeg definitivt lært den. Hvis du sikter mot 4 eller lavere så ville jeg definitivt prioritert andre deler av pensum.

Delbrøkoppspalting er en teknikk som vi blant annet kan bruke til å løse integraler med rasjonale uttrykk (se kapittel 2.2). Teknikken går ut på å skrive om en komplisert rasjonal funksjon til en sum av flere enkle rasjonale funksjoner. La $f (x)$ være en rasjonal funksjon bestående av polynomene $P$ og $Q$ slik at

f (x) = \frac{P (x)}{Q (x)}

For at vi skal kunne gjøre delbrøkoppspalting må $Q$ ha større grad enn $P$ . Dersom det ikke er tilfellet må du starte med å gjennomføre polynomdivisjonen $\frac{P (x)}{Q (x)}$ . Da sitter du igjen med et polynom som er enkelt å integrere, samt en rest som du kan bruke delbrøkoppspalting til å integrere.

Algoritmen for delbrøkoppspalting

Sjekk at nevner har høyere grad enn teller, ellers må du gjennomføre polynomdivisjon først
Faktoriser uttrykket i nevneren til $n$ faktorer
Sett uttrykket lik summen av $n$ brøker: $A$ over faktor 1, $B$ over faktor 2 og så videre opp til
Multipliser begge sider av likningen med fellesnevner
Sett inn $x$ -verdier som du ser at vil hjelpe deg med å bestemme $A$ , $B$ og så videre
Skriv om det opprinnelige uttrykket som summen av $n$ ledd
Integrer ledd for ledd

Jeg viser en delbrøkoppspalting med eksempelet $\int \frac{8}{x^{3} - 4 x} d x$ . Vi ser at nevneren har høyere grad enn teller, så vi kan gå videre til punkt 2 og faktoriserer nevneren.

\frac{8}{x^{3} - 4 x} = \frac{8}{x (x^{2} - 4)} = \frac{8}{x (x^{2} - 2^{2})} = \frac{8}{x (x - 2) (x + 2)}

Vi ser at vi har tre faktorer i nevneren. Vi går videre til punkt 3 og setter uttrykket vårt lik summen av tre brøker:

\frac{8}{x (x - 2) (x + 2)} = \frac{A}{x} + \frac{B}{x - 2} + \frac{C}{x + 2}

Vi går videre til punkt 4 og multipliserer med fellesnevneren $x (x - 2) (x + 2)$ på hver side

8 = A (x - 2) (x + 2) + B \cdot x (x + 2) + C \cdot x (x - 2)

Vi går videre til punkt 5 og ser at hvis vi setter inn $x = 0$ , $x = - 2$ og $x = 2$ så vil noen av leddene multipliseres med 0 og uttrykket vil bli forenklet

\begin{aligned} x = 0 gir 8 & = A (0 - 2) (0 + 2) + B \cdot 0 \cdot (0 + 2) + C \cdot 0 \cdot (0 - 2) \\ 8 & = - 4 A \\ A & = - 2 \\ x = - 2 gir 8 & = A (- 2 - 2) (- 2 + 2) + B \cdot (- 2) (- 2 + 2) + C \cdot (- 2) (- 2 - 2) \\ 8 & = A (- 4) (0) + B \cdot (- 2) (0) + C \cdot (- 2) (- 4) \\ 8 & = 8 C \\ C & = 1 \\ x = 2 gir 8 & = A (2 - 2) (2 + 2) + B \cdot 2 (2 + 2) + C \cdot 2 (2 - 2) \\ 8 & = A (0) (4) + B \cdot 2 (4) + C \cdot 2 (0) \\ 8 & = 8 B \\ B & = 1 \end{aligned}

Vi går videre til punkt 6 og setter opp uttrykket vårt

\frac{8}{x^{3} - 4 x} = \frac{- 2}{x} + \frac{1}{x - 2} + \frac{1}{x + 3}

Vi kan dermed gå videre til punkt 7 og faktisk integrere uttrykket ledd for ledd

\int \frac{8}{x^{3} - 4 x} d x = \int \frac{- 2}{x} d x + \int \frac{1}{x - 2} d x + \int \frac{1}{x + 2} d x = \underset{―}{\underset{―}{- 2 \ln | x | + \ln | x - 2 | + \ln | x + 2 |}}

Økonomi

Her lar vi $I (x)$ være inntektene ved salg av $x$ enheter og $K (x)$ være produksjonskostnadene ved produksjon av $x$ enheter. Overskuddet $O (x)$ er da gitt ved

O (x) = I (x) - K (x)

Grenseinntekt og grensekostnad

Grenseinntekten $I^{'} (x)$ er den deriverte av inntektsfunksjonen. Grenseinntekten $I^{'} (x)$ forteller oss omtrent hvor mye vi tjener på å selge én mer enhet.

Grensekostnaden $K^{'} (x)$ er den deriverte av kostnadsfunksjonen. Grensekostnaden $K^{'} (x)$ forteller oss omtrent hvor mye det koster å produsere én mer enhet.

Vi bruker også begrepene marginalinntekt og marginalkostnad.

Maksimalt overskudd

Vi har maksimalt overskudd når grenseinntekt er lik grensekostnad fordi

\begin{aligned} O^{'} (x) & = 0 \\ I^{'} (x) - K^{'} (x) & = 0 \\ I^{'} (x) & = K^{'} (x) \end{aligned}

Hvis du får flere løsninger så bør du sjekke hvilke løsninger som er toppunkter.

Enhetskostnader

Enhetskostnaden $E (x)$ fordeler produksjonskostnadene $K (x)$ på antall enheter $x$ .

E (x) = \frac{K (x)}{x}

Vi kan finne de laveste enhetskostnadene på tre måter:

Ved å løse likningen $E^{'} (x) = 0$
Ved å finne en tangent til kostnadsfunksjonen som går gjennom origo
Ved å løse $K^{'} (x) = E (x)$ . Utledningen for den siste formelen er som følger

\begin{aligned} E (x) & = \frac{K (x)}{x} \\ E^{'} (x) & = \frac{K^{'} (x) \cdot x - K (x) \cdot 1}{x^{2}} \end{aligned}

Vi setter uttrykket til den deriverte $E^{'} (x) = 0$ siden vi leter etter bunnpunktet til $E (x)$ .

\begin{aligned} E^{'} (x) = \frac{K^{'} (x) \cdot x - K (x) \cdot 1}{x^{2}} & = 0 \\ K^{'} (x) \cdot x - K (x) \cdot 1 & = 0 \\ K^{'} (x) \cdot x - K (x) & = 0 \\ K^{'} (x) \cdot x & = K (x) \\ K^{'} (x) & = \frac{K (x)}{x} \\ K^{'} (x) & = E (x) \end{aligned}

Etterspørsel

Etterspørselen $q$ er en funksjon av prisen $p$ slik at $q (p)$ . Etterspørselen er også lik antall solgte enheter $x$ slik at

x = q (p)

Inntektene er $pris \times antall solgte$ eller $I (x) = p \cdot x$ . Hvis vi bytter ut $x$ med $q (p)$ så får vi $I (p) = p \cdot q (p)$

På samme måte kan vi vise at kostnadene blir $K (x) = K (q (p))$ .

Sannsynlighet og statistikk

Diskrete sannsynlighetsfordelinger

I diskrete sannsynlighetsfordelinger så inneholder utfallsrommet til den stokastiske variabelen $X$ kun visse verdier. Ofte vil utfallsrommet til en diskret stokastisk variabel kun inneholde noen heltallsverdier.

Diskret sannsynlighetsfordeling

Dersom du kaster to mynter og lar $X$ være antall kron du får på disse kastene så er utfallsrommet ${0, 1, 2}$ . Det er ikke mulig å få 0,43 eller 1,783 mynt på to kast.

Uniform sannsynlighetsfordeling

I en uniform sannsynlighetsfordeling er sannsynligheten for alle utfallene like stor. Et eksempel på uniform sannsynlighetsfordeling er et terningkast: her har alle de seks sidene like stor sannsynlighet.

For å regne ut sannsynlighet ved uniform sannsynlighet tar vi

\frac{antall gunstige}{antall mulige}

Binomisk sannsynlighetsfordeling

Vi bruker binomiske fordelinger når vi kun har to ulike utfall. Vi bruker ofte bionomisk fordeling når vi definerer at en hendelse enten inntreffer eller så inntreffer den ikke.

Hvis vi gjør det samme binomiske forsøket flere ganger etter hverandre får vi en binomisk sannsynlighetsfordeling. Vi kaller antall forsøk for $n$ og observerer om hendelsen $A$ inntreffer eller ikke. Sannsynligheten for $A$ i hvert delforsøk er $p$ .

La $X$ være antallet ganger $A$ inntreffer på $n$ forsøk, da er sannsynligheten for at $A$ inntreffer nøyaktig $k$ ganger gitt ved

P (X = k) = (\binom{n}{k}) \cdot p^{k} \cdot (1 - p)^{n - k} = \frac{n!}{k! \cdot (n - k)!} \cdot p^{k} \cdot (1 - p)^{n - k}

Vilkår for binomisk sannsynlighetsfordeling

Alle delforsøkene må være uavhengige
Sannsynligheten for suksess, $p$ , er lik i alle delforsøkene

Hypergeometrisk sannsynlighetsfordeling

Vi bruker hypergeometrisk sannsynlighetsfordeling når vi har to ulike grupper med gjenstander og skal få et gitt antall av hver av dem. I hypergeometriske forsøk så er ikke delforsøkene uavhengige av hverandre.

Du har to typer objekter i en bolle, hvorav $n_{1}$ objekter er av type 1 og $n_{2}$ objekter er av type 2. Til sammen har du $n_{1} + n_{2} = n$ objekter. Du trekker $k$ objekter fra bollen. La $X$ være antallet objekter av type 1 blant de $k$ . Sannsynligheten for at du trekker nøyaktig $k_{1}$ objekter er gitt ved:

P (X = k_{1}) = \frac{(\binom{n_{1}}{k_{1}}) (\binom{n_{2}}{k_{2}})}{(\binom{n}{k})}

Forventningsverdi, varians og standardavvik

Forventningsverdi

Forventningsverdi er den gjennomsnittlige verdien vi kan forvente over lang tid. Forventningsverdien til $X$ finner vi med

μ = E (X) = \sum_{i = 1}^{n} x \cdot P (X = x)

Vi bruker vanligvis en tabell med sannsynlighetsfordelingen for å regne ut forventingsverdien. Nedenfor er et eksempel som viser sannsynlighetsfordelingen når $X$ er antall kron på ett myntkast.

$x$	$P (X = x)$	$x \cdot P (X = x)$
0	$\frac{1}{2}$	$0 \cdot \frac{1}{2} = 0$
1	$\frac{1}{2}$	$1 \cdot \frac{1}{2} = \frac{1}{2}$
Sum	1	$\frac{1}{2}$

Forventningsverdi i binomisk sannsynlighetsfordeling

I binomisk sannsynlighetsfordeling hvor antall forsøk er $n$ og sannsynligheten for suksess i hvert forsøk er $p$ , er forventningsverdien gitt ved:

μ = E (X) = n \cdot p

Forventningsverdi i kontinuerlige sannsynlighetsfordelinger

I kontinuerlige sannsynlighetsfordelinger finner vi forventningsverdien til $X$ ved å bestemme integralet

\int_{a}^{b} x \cdot f (x) d x

hvor $f$ er sannsynlighetstettheten (også kalt tetthetsfunksjonen) med definisjonsmengde $D_{f} = [a, b]$ .

Varians og standardavvik

Varians og standardavvik er spredningsmål – de måler variasjonen i observasjonene våre.

Varians og standardavvik

Standardavviket er kvadratroten av variansen: $σ = SD (X) = \sqrt{Var (X)}$
Standardavvik har samme måleenhet som observasjonene våre
Variansen har måleenheten til observasjonene opphøyd i andre

Variansen til $X$ finner vi med

Var (X) = \sum_{i = 1}^{N} ((x_{i} - μ)^{2} \cdot P (X = x_{i}))

Hvis vi ikke allerede har fått oppgitt forventningsverdien bruker vi vanligvis en tabell med sannsynlighetsfordelingen for å regne ut variansen. Nedenfor er et eksempel som viser sannsynlighetsfordelingen når $X$ er antall kron på ett myntkast. Jeg har valgt å først regne ut $(x - μ)^{2}$ , før jeg multipliserer med sannsynligheten i kolonne 5.

$x$	$P (X = x)$	$x \cdot P (X = x)$	$(x - μ)^{2}$	$(x - μ)^{2} \cdot P (X = x)$
$0$	$\frac{1}{2}$	$0 \cdot \frac{1}{2} = 0$	${(0 - \frac{1}{2})}^{2} = \frac{1}{4}$	$\frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8}$
$1$	$\frac{1}{2}$	$1 \cdot \frac{1}{2} = \frac{1}{2}$	${(1 - \frac{1}{2})}^{2} = \frac{1}{4}$	$\frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8}$
Sum	1	$\frac{1}{2}$		$\frac{1}{4}$

Fra summen i den femte kolonnen ser vi at $Var (X) = \frac{1}{4}$ , dette gir standardavviket $σ = \sqrt{Var (X)} = \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2}$ .

Varians i binomisk fordeling

I binomisk sannsynlighetsfordeling hvor antall forsøk er $n$ og sannsynligheten for suksess i hvert forsøk er $p$ , er variansen gitt ved

Var (X) = n \cdot p \cdot (1 - p)

Varians i kontinuerlige sannsynlighetsfordelinger

I kontinuerlige sannsynlighetsfordelinger finner vi variansen til $X$ ved å bestemme integralet

\int_{a}^{b} (x - μ)^{2} \cdot f (x) d x

hvor $f$ er sannsynlighetstettheten (også kalt tetthetsfunksjonen) med definisjonsmengde $D_{f} = [a, b]$ , og $μ$ er forventningsverdien til $X$ .

Regneregler for forventningsverdi og varians

La $X$ være en stokastisk variabel og $a$ og $b$ konstanter. Da har vi følgende regler

E (a \cdot X + b) = a \cdot E (X) + b og Var (a \cdot X + b) = a^{2} \cdot Var (X)

Regneregler for sum av stokastiske variabler

La $X_{1}, X_{2}, X_{3}, \dots, X_{n}$ være stokastiske variabler. Da gjelder

E (X_{1} + X_{2} + X_{3} + \dots + X_{n}) = E (X_{1}) + E (X_{2}) + E (X_{3}) + \dots + E (X_{n})

Hvis (og bare hvis) $X_{1}, X_{2}, X_{3}, \dots, X_{n}$ er uavhengige, så gjelder også

Var (X_{1} + X_{2} + \dots + X_{n}) = Var (X_{1}) + Var (X_{2}) + \dots + Var (X_{n})

Kontinuerlige sannsynlighetsfordelinger

I kontinuerlige sannsynlighetsfordelinger så inneholder utfallsrommet til den stokastiske variabelen $X$ alle verdier innenfor et intervall.

Sannsynligheten for at $X$ ligger innenfor et intervall $[a, b]$ er gitt ved

P (a < X < b) = P (a \leq X \leq b) = \int_{a}^{b} f (x) d x

Her er $f (x)$ sannsynlighetstettheten (eller tetthetsfunksjonen) til $X$ .

Punktsannsynlighet i kontinuerlige sannsynlighetsfordelinger

Legg merke til at $P (a < X < b) = P (a \leq X \leq b)$ .

Punktsannsynligheter i kontinuerlige sannsynlighetsfordelinger er lik null (altså $P (X = a) = 0$ ) siden

P (X = a) = \int_{a}^{a} f (x) d x = F (a) - F (a) = 0

Krav til sannsynlighetstettheten

f (x)

$f$ må ha en definisjonsmengde $D_{f} = [a, b]$
$f (x) \geq 0$
$\int_{a}^{b} f (x) d x = 1$

Normalfordelingen

Normalfordelingen er en kontinuerlig sannsynlighetfordeling med tetthetsfunksjon gitt ved

f (x) = \frac{1}{σ \sqrt{2 π}} e^{- \frac{(x - μ)^{2}}{2 σ^{2}}}

Definisjonsmengden er $D_{f} = R$ . Normalfordelingen er symmetrisk om linja $x = μ$ .

Standard normalfordeling

Alle normalfordelinger kan gjøres om til en standard normalfordeling med forventningsverdi $0$ og standardavvik $1$ . Vi bruker den stokastiske variabelen $Z$ i standard normalfordeling.

La $X$ være normalfordelt med forventningsverdi $μ$ og standardavvik $σ$ . For å bestemme $P (X < a)$ kan vi gjøre om $X \to Z$ ved å først regne ut en $z$ -verdi:

z = \frac{x - μ}{a}

Deretter bestemmer vi sannsynligheten $P (Z < z)$ ved å gå inn i tabellen med standard normalfordeling.

z

i standard normalfordeling

$z$ er antall standardavvik i standard normalfordeling. For eksempel betyr $z = - 2$ at grensa vår ligger to standardavvik til venstre for forventningsverdien.

Normalfordeling som tilnærming for binomiske fordelinger

Binomiske fordelinger blir tilnærmet normalfordelte når antall forsøk $n$ går mot uendelig, altså $lim_{n \to \infty}$ . Som tommelfingerregel sier vi at dersom $X$ er binomisk fordelt og $Var (X) \geq 5$ , så kan vi bruke normalfordeling som tilnærming for den binomiske fordelingen.

Forventningsverdi og varians er den samme for begge fordelingene.

μ = n p og Var (X) = n p (1 - p)

La $X$ være binomisk fordelt med $μ = n p$ og $σ = \sqrt{n p (1 - p)}$ . Hvis vi skal tilnærme med $X$ med normalfordeling må vi gjøre følgende halvkorreksjoner:

\begin{aligned} Binomisk & Normalfordelt \\ P (a < X < b) & ⟹ & P (a - 0, 5 < X < b + 0, 5) \\ P (X = a) & ⟹ & P (a - 0, 5 < X < a + 0, 5) \end{aligned}

Halvkorreksjon

Siden $P (X = a) = 0$ i normalfordelingen så er vi nødt til å gjøre en halvkorreksjon når vi finner sannsynligheter i binomiske fordelinger tilnærmet med normalfordelingen. Behovet for halvkorreksjon forsvinner når $n \to \infty$ .

Sentralgrensesetningen

Sentralgrensesetningen sier at dersom vi gjør tilstrekkelig mange forsøk, vil sannsynlighetsfordelingen til alle stokastiske variabler kunne tilnærmes med en normalfordeling.

La $X$ være en stokastisk variabel med forventningsverdi $μ$ og standardavvik $σ$ .

Vi lar $S$ være summen av $n$ delforsøk med $X$ slik at

S = X_{1} + X_{2} + \dots + X_{n}

Når $n \to \infty$ er summen $S$ tilnærmet normalfordelt med

\begin{aligned} E (S) & = n \cdot E (X) = n \cdot μ \\ Var (S) & = n \cdot Var (X) \\ SD (S) & = \sqrt{Var (S)} = \sqrt{n \cdot Var (X)} = \sqrt{n} \cdot \sqrt{Var (X)} = \sqrt{n} \cdot σ \end{aligned}

Denne tilnærmingen er best for store verdier av $n$ . Som tommelfingerregel gjelder sentralgrensesetningen når $n \geq 30$ .

Simuleringer med python

Vi bruker ofte Monte Carlo-simuleringer i programmer for å finne sannsynligheter som er vanskelig å bestemme ved regning. Prinsippet for slike simuleringer er:

Du definerer en hendelse $A$
Du gjennomfører et tilfeldig forsøk $N$ ganger
Du teller antall ganger $A$ inntreffer og kaller denne summen for $m$
Du beregner sannsynligheten ved: $P (A) \approx \frac{m}{N} = \frac{antall gunstige}{antall mulige}$

Dette er imidlertid ikke den ekte sannsynligheten, men $m / N$ gir en veldig god tilnærming når $N$ er høy. Prøv deg gjerne frem med stadig høyere $N$ (for eksempel 10000, 100 000, 1 000 000 og så videre), men stopp når du merker at programmet tar lang tid å kjøre.

Å trekke fra et statistisk fordeling

Vi kan trekke ut en tilfeldig prøve fra mange ulike statistiske fordelinger. I S2 skal vi fokusere på:

Uniform sannsynlighetsfordeling: alle utfallene er like sannsynlige
Binomisk sannsynlighetsfordeling
Hypergeometrisk sannsynlighetsfordeling
Normalfordeling

Vi bruker funksjoner fra biblioteket random til å gjøre uttrekk. Vi må derfor ha med linjen import random i toppen av programmene våre.

Trekke tilfeldig heltall

For å trekke et tilfeldig heltall i intervallet $[1, 6]$ (fra og med 1, til og med 6) så kan du bruke random.randint(a,b).

import random
tilfeldig_tall = random.randint(1,6)

Trekke tilfeldig desimaltall

For å trekke et tilfeldig desimaltall i intervallet $[0, 1 ⟩$ så kan du bruke random.random(). Hvis du trenger å ha et tilfeldig desimaltall i intervallet $[5, 15 ⟩$ så kan bare gange det tilfeldige tallet med 10 og legge til 5:

import random
tilfeldig_tall = random.random()
tilfeldig_tall2 = 10 * random.random() + 5

Trekke fra normalfordeling

For å trekke et tilfeldig tall fra en normalfordeling med forventningsverdi $μ = 180$ og standardavvik $σ = 7$ så kan du bruke random.gauss(mu, sigma).

import random
tilfeldig_tall = random.gauss(180, 7)

Eksempel på simulering fra eksempeleksamen høst 2022

På en skole er det 323 jenter og 301 gutter. $X$ er høyden på en tilfeldig valgt jente. $Y$ er høyden på en tilfeldig valgt gutt.

Anta at $X$ og $Y$ er normalfordelt med $μ_{X} = 168, μ_{Y} = 180, σ_{X} = 6, σ_{Y} = 8$ .

Lag et program som du kan bruke til å smulere sannsynligheten for at en tilfeldig valgt elev er høyere enn 175 cm.

import random

n_x = 323
n_y = 301
mu_x = 168
mu_y = 180
s_x = 6
s_y = 8

grense = 175
antall_simuleringer = 10000
antall_gunstige = 0

for i in range(antall_simuleringer):
    # Vi trekker en tilfeldig elev, men vi må finne ut om
    # eleven er gutt eller jente.
    # Det er 301 gutter. Hvis vi trekker et tilfeldig tall mellom
    # 1 og 301+323=624 så kan vi si at dersom tallet er mindre enn
    # eller lik 301, så er det en gutt.

    if (random.randint(1, n_x + n_y) <= n_y):
        # Her har vi altså trukket en gutt og vi trekker en tilfeldig gutt
        # fra en normalfordeling
        hoyde = random.gauss(mu_y, s_y)
    else:
        # ellers har vi trukket ei jente
        hoyde = random.gauss(mu_x, s_x)
    if (hoyde > grense):
        antall_gunstige += 1

sannsynlighet = antall_gunstige/antall_simuleringer

print(f"Sannsynligheten for å trekke en tilfeldig elev over 175 cm er "
      f"estimert til {sannsynlighet * 100:.1f} "
      f"med {antall_simuleringer} simuleringer")

Eksempel på simulering fra eksamen høst 2023

Høyden X til en tilfeldig valgt jente på 24 måneder er tilnærmet normalfordelt med forventningsverdi $E (X) = 87$ cm og standardavvik $SD (X) = 3, 3$ cm.

Høyden Y til en tilfeldig valgt gutt på 24 måneder er tilnærmet normalfordelt med forventningsverdi $E (Y) = 88$ cm og standardavvik $SD (Y) = 3, 1$ cm.

Lag et program som du kan bruke til å anslå sannsynligheten for at høyden til et tilfeldig valgt barn på 24 måneder er mindre enn 84 cm. Gå ut ifra at det er like mange jenter som gutter i populasjonen.

import random

EX = 87
SDX = 3.3
EY = 88
SDY = 3.1
N = 100_000
antall_gunstige = 0

for i in range(N):
    tilfeldig_tall = random.randint(1,2)

    if tilfeldig_tall == 1:
        # Vi har trukket en jente
        hoyde = random.gauss(EX, SDX)
    else:
        # Vi har trukket en gutt
        hoyde = random.gauss(EY, SDY)
    if hoyde < 84:
        antall_gunstige += 1

sannsynlighet = antall_gunstige / N
print(sannsynlighet)

Hypotesetesting

Vi bruker hypotesetester til å trekke slutninger om en hel populasjon basert på et utvalg eller stikkprøve.

I hypotesetester så bestemmer vi sannsynligheten for at observasjonene våre kan forekomme, gitt at en nullhypotese er sann.

Table: Begreper til hypotesetesting

Begrep	Forklaring
Hypotesetesting	Gjøre et utvalg/stikkprøve av en populasjon og finne ut om vi kan forkaste en nullhypotese.
Nullhypotese ( $H_{0}$ )	Den gjeldende hypotesen eller det vi ønsker å motbevise. Vi antar at denne er sann i hypotesetesting.
Alternativ hypotese ( $H_{A}$ )	Den hypotesen vi ønsker å teste ("bevise")
Testobservator ( $X$ )	En stokastisk variabel med en valgt sannsynlighetsfordeling forutsatt at $H_{0}$ er sann
Signifikansnivå ( $α$ )	Er som oftest 0,05. Det betyr at vi forkaster nullhypotesen i 5 % av tilfellene hvor vi ikke burde forkastet den (at vi gjør feil i 5 % av tilfellene).
$p$ -verdi	Sannsynligheten for observasjonen, gitt at $H_{0}$ er sann
Forkastningsmengde	De verdier av $X$ som gjør at $H_{0}$ forkastes
Aksepteringsmengde	De verdier av $X$ som gjør at $H_{0}$ beholdes
Venstresidig test	Tester om andelen er mindre enn nullhypotesen, altså $H_{A}$ : $p < p_{0}$
Høyresidig	Tester om andelen er større enn nullhypotesen, altså $H_{A}$ : $p > p_{0}$
Tosidig test	Tester om den egentlige verdien er ulik fra nullhypotesen $μ \neq μ_{0}$

Algoritme for hypotesetester

Sett opp nullhypotese og alternativ hypotese. Nullhypotesen er det vi ønsker å motbevise.
Anta at nullhypotesen er sann og sett opp sannsynlighetsfordelingen for $X$
Regn ut $p$ -verdien (sannsynligheten for å få observasjonene gitt at nullhypotesen er sann)
Sammenlign $p$ -verdien med signifikansverdien $α$ .
- $p < α$ betyr at vi forkaster $H_{0}$ . Sannsynligheten for at observasjonene skal oppstå tilfeldig er mindre enn signifikansnivået.
- $p > α$ betyr at vi ikke forkaster $H_{0}$ . Sannsynligheten for at observasjonene skal oppstå tilfeldig er større enn signifikansnivået.
Skriv konklusjon

Hypotesetesting av andeler

Vi undersøker om sannsynligheten $p$ i en binomisk fordeling har en bestemt verdi ved å teste $H_{0} : p = p_{0}$ mot

Venstresidig test $H_{A} : p < p_{0}$ .
Høyresidig test $H_{A} : p > p_{0}$
Dobbeltsidig test $H_{A} : p \neq p_{0}$

Vi velger $X$ som testobservator og tar en stikkprøve der $X$ får verdien $a$ .
Vi regner ut $p$ -verdien^[3]
- Ved venstresidig test så beregner vi $p$ -verdien $P (X < a)$ .
- I en høyresidig test regner vi ut $p$ -verdien $P (X > a)$ .
- I en dobbeltsidig test regner vi ut $p$ -verdien $P (X < a) + P (X > a)$ .
Hvis $p < α$ så forkaster vi $H_{0}$

Hypotesetest av andel ved å bruke normalfordeling

Siden binomiske fordelinger kan være tilnærmet normalfordelte (se kapittel 6.4.2), så kan vi bruke normalfordelingen til å teste andeler når $Var (X) \geq 5$ .

I hypotesetesten bruker vi da en normalfordeling med $μ = n p$ og $σ = \sqrt{n p (1 - p)}$ .

Hypotesetesting av gjennomsnitt

La $\bar{X}$ være gjennomsnittsverdien i en stikkprøve bestående av $n$ elementer av den stokastiske variabelen $X$ . $X$ har forventningsverdi $μ$ og standardavvik $σ$ . Forventningsverdien og standardavviket til $\bar{X}$ er da

\begin{aligned} E (\bar{X}) & = E (X) = μ \\ SD (\bar{X}) & = \frac{SD (X)}{\sqrt{n}} = \frac{σ}{\sqrt{n}} \end{aligned}

I hypotesetesten vår så bruker vi en normalfordeling med $E (\bar{X}) = μ$ og $SD (\bar{X}) = \frac{σ}{\sqrt{n}}$ .

Merk at python-lister begynner på indeks 0. Det vil si at for å hente ut det første elementet i ei liste som heter min_liste så skriver vi min_liste[0]. For å hente du det fjerde elementet i lista skriver vi min_liste[3]. ↩︎
Denne formelen tror jeg ikke du trenger å pugge til del 1 av eksamen. ↩︎
$p$ -verdi og sannsynligheten $p$ i binomisk modell er ikke det samme. ↩︎